
As we continue marching towards final adoption of FASB’s ASC-326 (a.k.a., Current Expected Credit Loss, or CECL for short) in January 2023, community banks and credit unions are fully engaged. When CECL was first released back in 2016, the prevailing thought was that achieving compliance basically meant choosing a model and filling it with data. Everyone thought the biggest challenge would be figuring out how to bridge the gap between the allowance for loan and lease losses (ALLL) calculated by the incurred loss methodology to the CECL ALLL. Now, financial institutions are discovering that complex risk models require some maintenance and that they need to fully understand how a model works to know whether its results accurately reflect the risk in their loan portfolio.
What tools do financial institutions have to ensure that their calculated CECL results accurately reflect the risk in their portfolio? Models are built by humans and, as such, share an undeniable characteristic with their builders: they are fallible.
All models have weaknesses, even the ‘sophisticated’ ones. The accounting standards acknowledge this fact and therefore allow practitioners to make qualitative adjustments (i.e., Q factors) to calculated results. Q factors are one tool financial institutions can use to assess risk accuracy but need to be used appropriately. They must:
One can see how it could be tempting to use Q factors to bridge any gap between incurred loss methodology results and CECL results. We have observed this within our client base, albeit rarely; the accounting standard is clear about the need to provide quantitative support for Q factors. Use of Q factors also invites unwanted scrutiny from an auditor or examiner. So, in practice, their use is stigmatized.
If the support for qualitative adjustments is ultimately quantitative, then a perhaps different quantitative model is a better option.
The gold standard for CECL models is Probability of Default/Loss Given Default models (PD/LGD). The benefits of employing these models are well known. Their use is directly referenced by Basel II and the Financial Accounting Standards Board (FASB). PD/LGD models make use of unique loan characteristics that have high correlation to loss and severity:
The Instrument level results produced by PD/LGD models can also be integrated with other management analyses:
But one of the primary weaknesses of PG/LGD models is the breadth and depth of data required to produce good results. The data must have:
Here are two common scenarios where an additional model beyond PD/LGD is needed (along with clarification on which model type is most appropriate).
PD/LGD models require multiple credit cycles of history to calculate correlations between economic indicators and loan losses. To build a model with two credit cycles, we would need instrument-level data back to the year 2000. This is simply not practical. Consequently, most models will rely on publicly available historic data (peer data) to create these correlations.
What happens when a specific financial institution (FI) portfolio loss history looks nothing like peer group loss history? Consider the bank that has low- or no charge offs over the most recent five-year period. Given the recent benign credit environment leading up 2020, this is a common occurrence. Use of peer data correlations to forecast expected losses would cause the CECL reserves to be overstated by millions of dollars. When this FI adopts CECL in 2023, their provision expense under PG/LGD would impair capital by almost $22 million.
|
Metric |
PG / LGD |
Roll Rate |
Vintage |
Time Series |
|
Outstanding Balance |
$398,745,894 |
$398,745,894 |
$398,745,894 |
$ 398,745,894 |
|
Historic 12-Month Loss Rate (Net) |
0.02% |
0.02% |
0.02% |
0.02% |
|
FAS-5 ALLL Rate |
0.15% |
0.15% |
0.15% |
0.15% |
|
FAS-5 ALLL Amount |
$598,119 |
$598,119 |
$598,119 |
$598,119 |
|
CECL 12 Month Expected Loss Rate (Net) |
1.75% |
0.17% |
1.89% |
1.98% |
|
CECL Lifetime Loss Rate (Net) |
5.60% |
0.54% |
6.05% |
6.34% |
|
CECL Reserve Amount (Net) |
$22,329,770 |
$2,169,178 |
$24,116,152 |
$25,264,540 |
Closing that gap with a Q factor isn’t an option. Instead, use a model that is not based on regression or peer data. A roll rate model generates expected losses by measuring the probability of a loan rolling from one delinquency bucket to another (30 to 60, 60 to 90, 90 back to 30, etc.). Roll rate model results are driven by the FI’s unique delinquency and loss experience. The industry is familiar with roll rate models, and they provide completely valid results in this instance. Roll rate does have some weaknesses but may give a better representation of the risk in this example.
Instrument-level loan characteristics (LTV, FICO, DSCR) provide strong correlations to losses and severity of loss. PD/LGD models make great use of these factors to differentiate loss expectations on the FI’s loans compared to the pool loans. With that data missing, the modeler loses the benefit of the granularity found in PD/LGD. There is, however, another strength of PG/LGD that does not require loan level detail, that is, the loan product lifecycle, which is also associated with vintage models.
Separate from all other influencers of loss, the Probability of Default (PD) of a loan changes over time. Each loan type has a general lifecycle to it. Some, like auto loans, are very predictable.
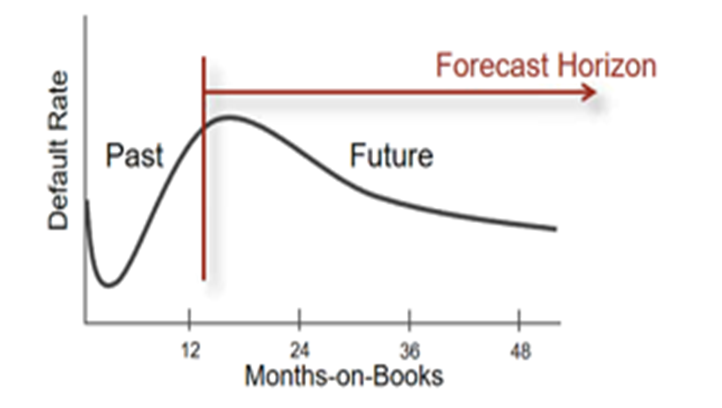
PD is typically very low in the beginning of the life cycle. The peak PD differs for each product, but after the peak, PD steadily declines over time. A vintage model is very suitable in this situation. The user gives up the granularity of PD/LGD, but still retains the strengths common to both models:
As pointed out in the beginning of this post, all models have weaknesses. We don’t have to apologize for them or cover them up. On the contrary, our role as risk managers is to call attention to them. By having multiple models available to us and understanding how each model works, we make our best effort at communicating the risk in the portfolio to our stakeholders.
Stay up to date with the latest people-inspired innovation at Jack Henry.
.svg)

Learn more about people-inspired innovation at Jack Henry.
Who We Serve
What We Offer
Who We Are